Dado los números de un reloj digital, por ejemplo:
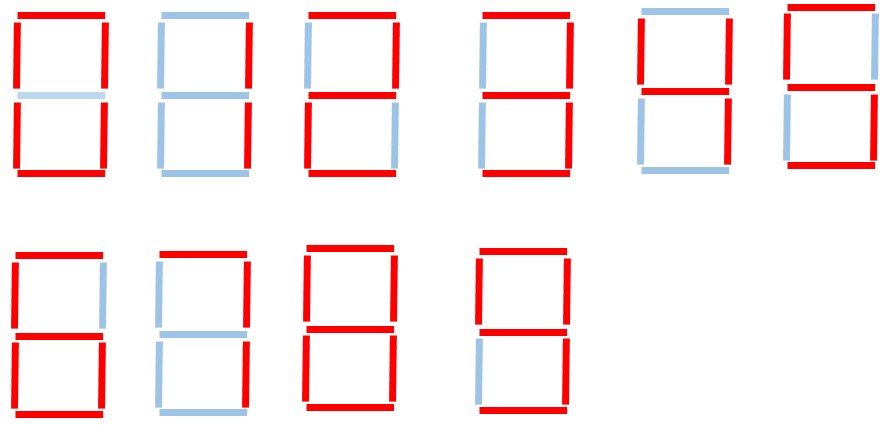
Puede interpretarlos como 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Este problema se abordó en mi libro Redes Neuronales y fue resuelto usando un percetrón multicapa.
Se quiere resolver con un algoritmo genético que dado ese número al estilo reloj digital se pueda deducir el número como tal.
Para iniciar se pone un identificador a cada barra.
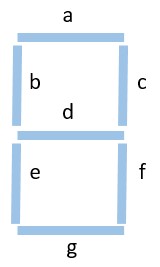
Luego se le da un valor de “1” a la barra que queda en rojo al construir el número y “0” a la barra que queda en azul claro. Por ejemplo:
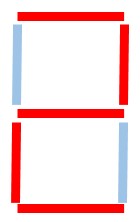
Así se representa el dibujo de cada número de un reloj digital:
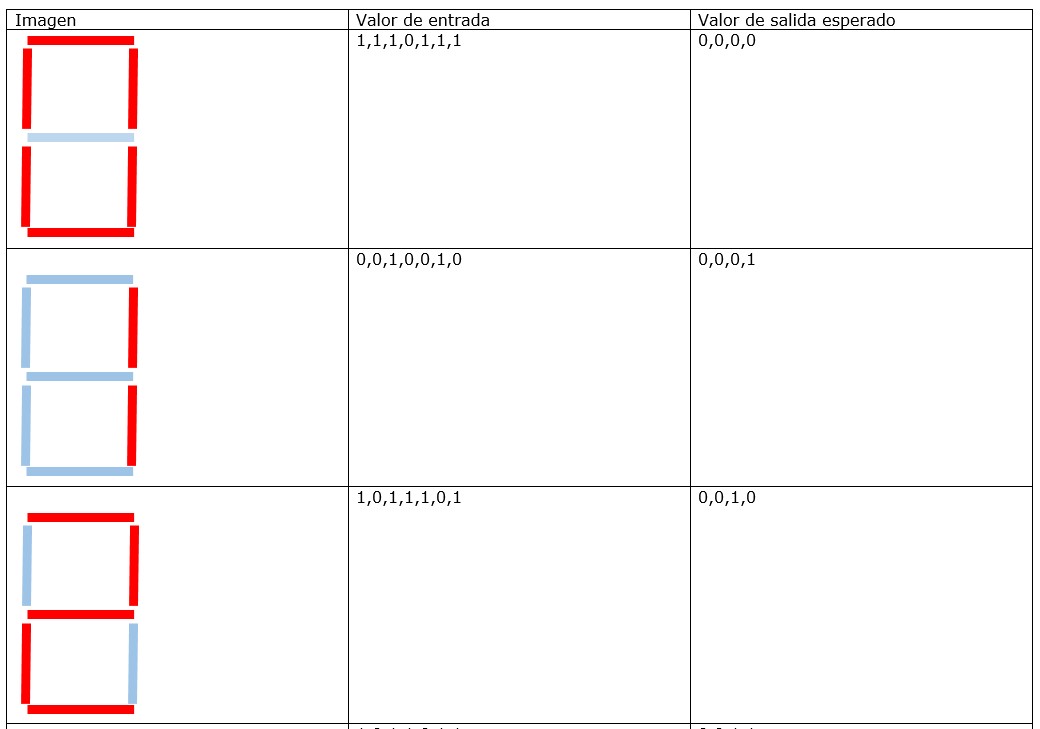
En código fuente
Entradas = new int[][] {
new int[] { 1, 1, 1, 0, 1, 1, 1 }, // Número 0
new int[] { 0, 0, 1, 0, 0, 1, 0 }, // Número 1
new int[] { 1, 0, 1, 1, 1, 0, 1 }, // Número 2
new int[] { 1, 0, 1, 1, 0, 1, 1 }, // Número 3
new int[] { 0, 1, 1, 1, 0, 1, 0 }, // Número 4
new int[] { 1, 1, 0, 1, 0, 1, 1 }, // Número 5
new int[] { 1, 1, 0, 1, 1, 1, 1 }, // Número 6
new int[] { 1, 0, 1, 0, 0, 1, 0 }, // Número 7
new int[] { 1, 1, 1, 1, 1, 1, 1 }, // Número 8
new int[] { 1, 1, 1, 1, 0, 1, 1 } // Número 9
};
Valor del número en notación binaria
SalidasEsperadas = new int[][] {
new int[] { 0, 0, 0, 0 }, //0
new int[] { 0, 0, 0, 1 }, //1
new int[] { 0, 0, 1, 0 }, //2
new int[] { 0, 0, 1, 1 }, //3
new int[] { 0, 1, 0, 0 }, //4
new int[] { 0, 1, 0, 1 }, //5
new int[] { 0, 1, 1, 0 }, //6
new int[] { 0, 1, 1, 1 }, //7
new int[] { 1, 0, 0, 0 }, //8
new int[] { 1, 0, 0, 1 } //9
};
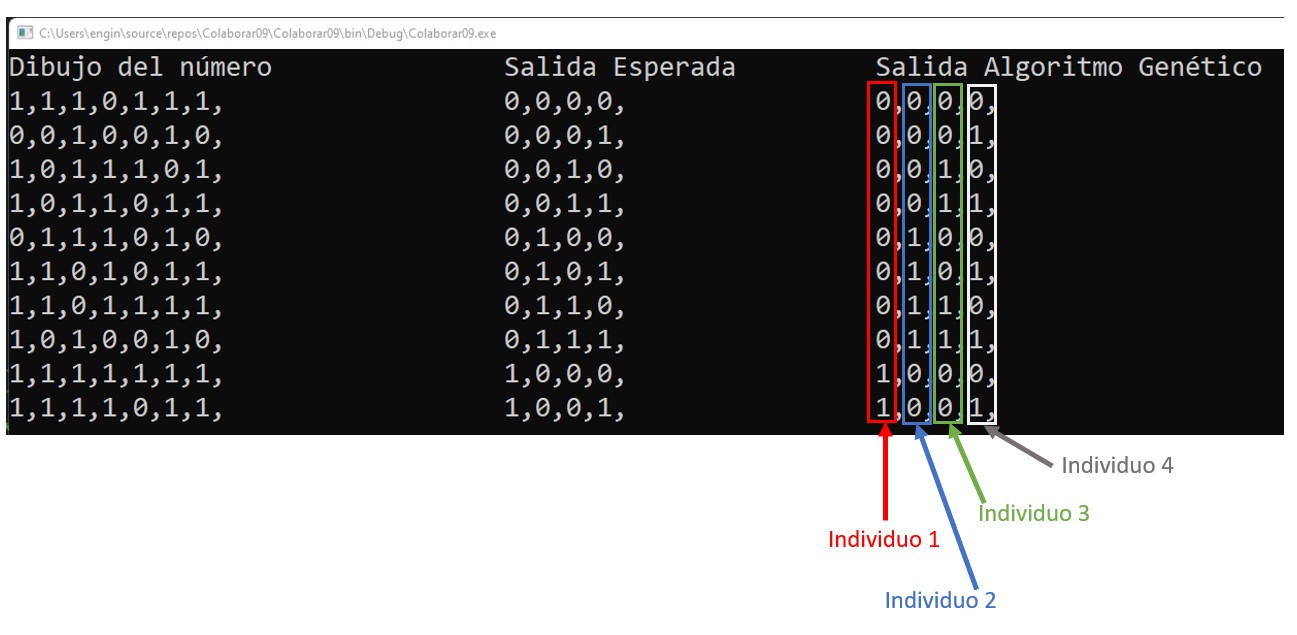
Se usa colaboración entre distintos individuos.
I. Para una población 1:
Significa que si se ingresa 1, 1, 1, 0, 1, 1, 1 (primer registro de entradas) se obtiene 0 (primer valor del primer registro de salidas Esperadas)
Si se ingresa 0, 0, 1, 0, 0, 1, 0 (segundo registro de entradas) se obtiene 0 (primer valor del segundo registro de salidas Esperadas)
Si se ingresa 1, 0, 1, 1, 1, 0, 1 (tercer registro de entradas) se obtiene 0 (primer valor del tercer registro de salidas Esperadas)
y así sucesivamente...
II. Para una población 2:
Significa que si se ingresa 1, 1, 1, 0, 1, 1, 1 (primer registro de entradas) se obtiene 0 (segundo valor del primer registro de salidas Esperadas)
Si se ingresa 0, 0, 1, 0, 0, 1, 0 (segundo registro de entradas) se obtiene 0 (segundo valor del segundo registro de salidas Esperadas)
Si se ingresa 1, 0, 1, 1, 1, 0, 1 (tercer registro de entradas) se obtiene 0 (segundo valor del tercer registro de salidas Esperadas)
y así sucesivamente...
III. Para una población 3:
Significa que si se ingresa 1, 1, 1, 0, 1, 1, 1 (primer registro de entradas) se obtiene 0 (tercer valor del primer registro de salidas Esperadas)
Si se ingresa 0, 0, 1, 0, 0, 1, 0 (segundo registro de entradas) se obtiene 0 (tercer valor del segundo registro de salidas Esperadas)
Si se ingresa 1, 0, 1, 1, 1, 0, 1 (tercer registro de entradas) se obtiene 1 (tercer valor del tercer registro de salidas Esperadas)
y así sucesivamente...
IV. Para una población 4:
Significa que si se ingresa 1, 1, 1, 0, 1, 1, 1 (primer registro de entradas) se obtiene 0 (cuarto valor del primer registro de salidas Esperadas)
Si se ingresa 0, 0, 1, 0, 0, 1, 0 (segundo registro de entradas) se obtiene 1 (cuarto valor del segundo registro de salidas Esperadas)
Si se ingresa 1, 0, 1, 1, 1, 0, 1 (tercer registro de entradas) se obtiene 0 (cuarto valor del tercer registro de salidas Esperadas)
y así sucesivamente...
Son 4 poblaciones, cada población generará un individuo que cumpla con las salidas esperadas. Luego al juntar los 4 individuos, se interpreta el reloj digital.