Dada una serie de datos X, Y donde X no se repite. Hallar la función Y = F(X) que mejor se ajuste a esa serie de datos. Por ejemplo, se tienen los datos (1, 2); (2, 4); (3, 6); (4, 8); se deduce que la mejor función es Y = 2*X.
¿Pero cuando hay cientos o miles de datos X, Y y la función no es fácil de encontrar?
En el pasado se abordó buscar esa única función usando algoritmos genéticos. En este software se cambia el enfoque y es que se divide la serie de datos, al principio por la mitad. A la primera mitad se le calcula una función F(X) que mejor se aproxime, a la segunda mitad se le calcula una funcíon G(X) que mejor se aproxime. Se obtendría dos funciones, el inicio de la colaboración. Más adelante la serie de datos se divide en tres partes iguales y se calcularía las funciones F(X), G(X), H(X) para cada parte y así sucesivamente.
Estos son los pasos en detalle:
1. Generar una sola función Y = F(X) que mejor ajuste a todo el conjunto de datos.
2. Generar una función Y = F(X) que ajuste a la primera mitad del conjunto datos y luego generar una segunda función Y = G(X) que ajuste a la segunda mitad.
3. Generar una función Y = F(X) que ajuste al primer tercio del conjunto datos, luego generar una segunda función Y = G(X) que ajuste al segundo tercio y una última función Y=H(X) que ajuste al tercio final.
4. Y así sucesivamente
Se va a utilizar una función de este estilo:
Y = (Seno(a*(1-X)^4 + b*(1-X)^3 + c*(1-X)^2 + d*(1-X) + e + f*X + g*X^2 + h*X^3 + i*X^4) + 1)/2
Los valores de Y están comprendidos entre 0 y 1, eso significa que el conjunto de datos debe estar normalizado entre 0 y 1.
En el algoritmo genético, como se trabaja con una población, cada individuo de la población es una función de ese estilo, pero con distintos valores a, b, c, d, e, f, g, h, i. El objetivo es hallar el individuo que se ajuste mejor a los datos (saber que valores o coeficientes a,b,c,d,e,f,g,h,i permiten el mejor ajuste).
¿Por qué esa función de ese estilo? Porque en la naturaleza no hay valores de crecimiento infinito Y, se llega a un tope (por leyes físicas) y comenzaría a disminuir, y podría aumentar de nuevo para luego volver a disminuir, es decir, un comportamiento cíclico, que se representa con una función sinusoidal. También Y podría a tender a cero y esa función puede mostrar ese comportamiento.
¿Podría ser otro tipo de función? Por supuesto, podría usarse coseno o cualquier otra función (recomendado tener en cuenta el comportamiento cíclico) y tener más coeficientes. Cabe recordar que una función muy compleja o con una gran cantidad de coeficientes puede hacer más lento evaluarla, pero muy pocos coeficientes generan muy poca variedad.
El algoritmo genético trabaja así:
Paso 1: Dada una serie de valores (X, Y) donde X es la variable independiente y Y la variable dependiente se usará un algoritmo evolutivo para determinar cuál expresión matemática de tipo Y=F(X) logra ajustarse a esos datos.
Paso 2: Los individuos son del tipo: Y = (Math.Sin(a*(1-x)^4 + b*(1-x)^3 + c*(1-x)^2 + d*(1-x) + e + f*x + g*x^2 + h*x^3 + i*x^4) + 1)/2
Paso 3: La población se compone de N individuos generados al azar
Paso 4: El proceso evolutivo es:
a. Seleccionar dos individuos al azar
b. Evaluar cada individuo escogido que tanto ajusta con la salida esperada
c. El individuo con mejor ajuste sobrescribe al de menor ajuste
d. El nuevo individuo (copia del mejor) se modifica al azar
Paso 5: El proceso evolutivo se repite N veces
Paso 6: Se escanea toda la población por el mejor individuo (mejor ajuste)
Paso 7: El mejor individuo muestra sus valores de salida dado los valores de entrada
Resultado de una prueba de ejemplo
Se genera un conjunto de datos de 2000 registros (X, Y) y se ejecuta el algoritmo genético para hallar una sola función que cubra todo el conjunto de datos, luego con dos individuos (primera mitad y segunda mitad), luego con tres individuos (primer tercio, segundo tercio y último tercio) y así sucesivamente:
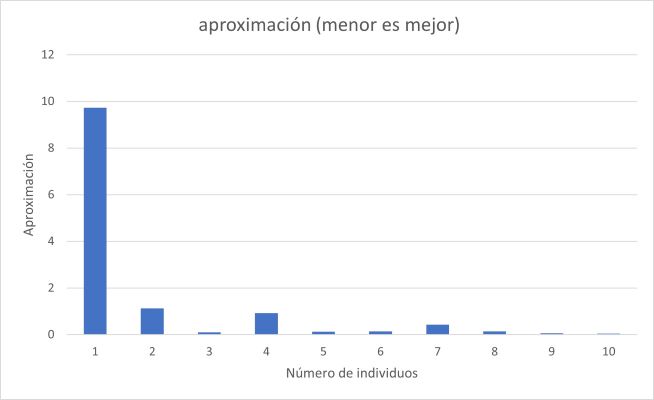
Este es el gráfico obtenido. Valor menor significa mejor ajuste.
Número de individuos por población: 200
Número de ciclos a evaluar: 10000
| Número de funciones que cubren los datos | Aproximación (menor es mejor) |
|---|
| Sólo una(1) función para toda la serie de datos | 9,72667259630838 |
| Dos(2) funciones, la serie se divide mitad y mitad | 1,12793365536098 |
| Tres(3) funciones, la serie se divide en tercios | 0,0937628784160977 |
| Cuatro(4) funciones | 0,914439257015682 |
| Cinco(5) funciones | 0,126971590478581 |
| Seis(6) funciones | 0,133483004063954 |
| Siete(7) funciones | 0,42821748238329 |
| Ocho(8) funciones | 0,144078634205807 |
| Nueve(9) funciones | 0,0570441846308953 |
| Diez(10) funciones | 0,0462012255833265 |